A Neat Hack

I admit to being unreasonably pleased with the following trick: The KenKen solver we’ve built and tuned can be generalized to solve Sudoku, including jigsaw Sudoku, with a 9-character change to its source code.

The Change

First, get the most recent version of the solver. Then, redefine the Puzzle.lut class-level member s.t. the Puzzle class looks like this:

class Puzzle(object):
	lut = {'!':Assert, '+':Sum, '-':Diff, '*':Prod, '/':Div, 's':Set}
	def __init__(self, fn):
		# Parse file
		lines = [l.split() for l in file(fn, 'rb').read().strip().split('\n')]
		if (lines[0][0] != '#'):
			raise Exception('Puzzle definitions must begin with a size ("#") line')
		self.size	= int(lines[0][1])
		self.cages	= [self.lut[l[0]](*l[1:]) for l in lines[1:]]

The only change is the addition of the ‘s’ -> Set mapping in the lut dictionary. This change will let us define uniqueness constraints in our puzzle definitions.

Jigsaw Sudoku

Jigsaw Sudoku is like normal Sudoku, except that the third uniqueness constraint (in addition to those for rows and columns) is associated with irregular cages, instead of regular boxes. Here is an example:

We would define this puzzle in our definition language as follows:

#	9
s	0	A1 A2 A3 B2 B3 C3 C4 D3 D4
s	0	A4 A5 A6 A7 A8 B4 B5 B6 B8
s	0	A9 B7 B9 C7 C8 C9 D7 D8 D9
s	0	B1 C1 C2 D1 D2 E1 E2 E3 F3
s	0	C5 C6 D5 D6 E4 E5 E6 E7 F6
s	0	E8 E9 F7 F8 F9 G8 G9 H8 H9
s	0	F1 F2 F4 F5 G1 G2 G3 G4 H4
s	0	G5 G6 G7 H5 H6 H7 I7 I8 I9
s	0	H1 H2 H3 I1 I2 I3 I4 I5 I6
!	7	A2
!	6	A5
!	3	A7
!	1	A8
!	4	B1
!	7	B8
!	1	B9
!	8	C2
!	1	D1
!	8	D3
!	7	D5
!	5	D8
!	2	D9
!	3	E1
!	8	F1
!	5	F2
!	9	F5
!	1	F7
!	4	F9
!	9	G8
!	9	H1
!	4	H2
!	5	H9
!	1	I2
!	5	I5
!	4	I8

If this description were stored in a file in the current working directory named “jig.txt”, and the solver was stored in a file on the import path named “neknek_2.py”, we could solve the puzzle with the following Python code:

import neknek_2
neknek_2.print_solution(neknek_2.solve(neknek_2.Puzzle("jig.txt")))

The solution, incidentally, is:

5 | 7 | 9 | 2 | 6 | 4 | 3 | 1 | 8
--+---+---+---+---+---+---+---+--
4 | 3 | 2 | 5 | 8 | 9 | 6 | 7 | 1
--+---+---+---+---+---+---+---+--
6 | 8 | 1 | 4 | 2 | 5 | 7 | 3 | 9
--+---+---+---+---+---+---+---+--
1 | 9 | 8 | 6 | 7 | 3 | 4 | 5 | 2
--+---+---+---+---+---+---+---+--
3 | 2 | 5 | 9 | 4 | 1 | 8 | 6 | 7
--+---+---+---+---+---+---+---+--
8 | 5 | 7 | 3 | 9 | 6 | 1 | 2 | 4
--+---+---+---+---+---+---+---+--
2 | 6 | 4 | 7 | 1 | 8 | 5 | 9 | 3
--+---+---+---+---+---+---+---+--
9 | 4 | 6 | 1 | 3 | 7 | 2 | 8 | 5
--+---+---+---+---+---+---+---+--
7 | 1 | 3 | 8 | 5 | 2 | 9 | 4 | 6

It is a little cumbersome to use the solver in this way; in particular, our puzzle description language isn’t well suited to puzzles with so many constants. It works, though.

Regular Sudoku

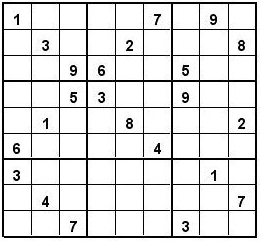
Normal Sudoku puzzles, of course, are just special cases of Jigsaw Sudoku. Here’s an example of a Sudoku puzzle – specifically, what has been claimed to be the hardest known Sudoku puzzle:

And here is how we’d represent it:

#	9
s	0	A1 A2 A3 B1 B2 B3 C1 C2 C3
s	0	A4 A5 A6 B4 B5 B6 C4 C5 C6
s	0	A7 A8 A9 B7 B8 B9 C7 C8 C9
s	0	D1 D2 D3 E1 E2 E3 F1 F2 F3
s	0	D4 D5 D6 E4 E5 E6 F4 F5 F6
s	0	D7 D8 D9 E7 E8 E9 F7 F8 F9
s	0	G1 G2 G3 H1 H2 H3 I1 I2 I3
s	0	G4 G5 G6 H4 H5 H6 I4 I5 I6
s	0	G7 G8 G9 H7 H8 H9 I7 I8 I9
!	1	A1
!	3	B2
!	9	C3
!	6	C4
!	2	B5
!	7	A6
!	9	A8
!	8	B9
!	5	C7
!	6	F1
!	1	E2
!	5	D3
!	3	D4
!	8	E5
!	4	F6
!	9	D7
!	2	E9
!	3	G1
!	4	H2
!	7	I3
!	1	G8
!	7	H9
!	3	I7

If this description were stored in a file in the current working directory named “aie.txt”, and the solver was stored in a file on the import path named “neknek_2.py”, we could solve the puzzle with the following Python code:

import neknek_2
neknek_2.print_solution(neknek_2.solve(neknek_2.Puzzle("aie.txt")))

The solution, incidentally, is:

1 | 6 | 2 | 8 | 5 | 7 | 4 | 9 | 3
--+---+---+---+---+---+---+---+--
5 | 3 | 4 | 1 | 2 | 9 | 6 | 7 | 8
--+---+---+---+---+---+---+---+--
7 | 8 | 9 | 6 | 4 | 3 | 5 | 2 | 1
--+---+---+---+---+---+---+---+--
4 | 7 | 5 | 3 | 1 | 2 | 9 | 8 | 6
--+---+---+---+---+---+---+---+--
9 | 1 | 3 | 5 | 8 | 6 | 7 | 4 | 2
--+---+---+---+---+---+---+---+--
6 | 2 | 8 | 7 | 9 | 4 | 1 | 3 | 5
--+---+---+---+---+---+---+---+--
3 | 5 | 6 | 4 | 7 | 8 | 2 | 1 | 9
--+---+---+---+---+---+---+---+--
2 | 4 | 1 | 9 | 3 | 5 | 8 | 6 | 7
--+---+---+---+---+---+---+---+--
8 | 9 | 7 | 2 | 6 | 1 | 3 | 5 | 4

Of course, using the solver this way is really silly; not only is our puzzle description language poorly suited to listing all those constants, but the cage constraints are implicit in regular Sudoku, and don’t need to be specified. I still think it’s neat that the code can be so easily made to support these additional types of puzzles.